알고리즘 공부를 하다가, 다익스트라 알고리즘 관련한 부분에서 다음과 같은 내용을 마주했다.
다익스트라의 최초 구현에서는 시간 복잡도가 O(V^2)였으나, 현재는 너비 우선 탐색 시 가장 가까운 순서를 찾을 때 우선순위 큐를 적용하여 이 경우 시간 복잡도는 O((V+E)log V), 모든 정점이 출발지에서 도달이 가능하다면 최종적으로 O(E log V)가 된다.
<파이썬 알고리즘 인터뷰> 372p
어... 음...
최단경로 뿐만 아니라 전반적인 그래프 활용 알고리즘에서 시간복잡도 표기가 잘 이해가 안 되는 느낌이었는데, 그냥 대충 이런 느낌이네~ 하고 넘어갔더니 이렇게 자료구조 활용에 따른 최적화 같은 중요한 내용도 잘 안 와닿게 된다. 그래서 위 문장을 하나하나 뜯어보면서 풀이해 보려고 한다.
이 글에서는 다익스트라 알고리즘의 기본 원리와 구현을 깊게 설명하지는 않고(그러면 언제 다 쓸 수 있을지 모른다...) 시간 복잡도를 계산하는 측면에서만 탐구해 보았다. 다익스트라 알고리즘의 기본 동작 방식은 다른 블로그를 참고하면 많은 내용을 찾아볼 수 있다.
그래프 시간 복잡도에서 'V'와 'E'의 의미
그래프 관련한 알고리즘 문제들의 해설을 보다 보면 자주 등장하는 게 V와 E라는 표기다. 이건 당연히 Vertex와 Edge의 약어다. 참 쉽죠? 근데 (나만 그런지 모르겠지만) 이 두 용어가 의외로 꽤 헷갈린다. 정리하면 Vertex는 그래프의 각 노드(정점)다. 그리고 Edge가 각 노드를 잇는 선(간선)이다. 뭔가 내 머릿속에서는 Edge라고 하면 기본적으로 '가장자리'를 떠올리게 되는데 사실 Vertex와 Edge는 기하학에서 입체도형을 이루는 각 꼭짓점과 모서리를 의미한다. 그걸 떠올리면 좀 더 명확해진다.

자, 그럼 O((V+E)log V)라는 표기는 O((노드의 개수 + 간선 개수)log 노드의 개수)로 정리할 수 있다. 근데 E를 '한 점에 연결되어 있는 간선 개수'로 표현한 자료도 있고, '전체 그래프의 간선 개수'로 표현한 자료도 있다. 이 글에서는 후자를 기준으로 적는다. 이제 본격적으로 시간복잡도 분석을 해 보자.
배열 구현의 시간 복잡도
다익스트라는 이 알고리즘 구현한 사람 이름인데, 다익스트라를 처음 구현했을 때는 트리 기반의 최소힙을 쓰지 않았고, 그냥 배열로 구현했다. 여기서 말하는 queue는 이름은 큐지만 그냥 배열이라고 생각하면 편하다.
1) 먼저 (노드 x, 노드 x까지의 현재 최소 거리)의 형태로 모든 노드의 값을 queue에 추가한다.
맨 처음에는 (시작점, 0)일 것이고, 나머지는 (노드 x, 무한대)의 형태로 초기화될 것이다. 앞으로 BFS로 탐색하면서 각 노드로 가는 최소 거리는 계속해서 업데이트 되겠지만, 우선 가장 처음에 이렇게 모든 정점의 값을 넣어놓는 데 O(V), 즉 정점의 개수만큼 시간이 걸린다.
(해당 정점에 이미 방문했는지를 알려 주는 자료구조도 필요하지만, 방문 여부를 체크하는 건 시간복잡도 측면에서 큰 문제는 아니므로 이 글에서는 우선 넘어가도록 하자.)
2) queue에 들어있는 (노드 x, 노드 x까지의 현재 최소 거리) 중에서 가장 짧은 거리를 가진 노드 x를 찾아서, 해당 노드에 아직 방문하지 않았을 경우 해당 노드 x와 연결된 노드까지의 거리 값을 업데이트한다.
우선순위 큐를 사용하지 않은 구현에서는, 배열에서 가장 짧은 거리를 찾는 데에 이미 O(V)만큼의 시간이 소요된다. 배열이니까 모든 값을 뒤져야 하기 때문이다.
3) 이 과정을 모든 노드를 방문할 때까지 반복한다.
즉, O(V)의 시간이 걸리는 '거리 최소값 찾고 업데이트하기'라는 연산을 또 노드의 개수만큼 처리하게 된다. 즉 O(V)다.

따라서 이 경우의 시간복잡도는 1) + 2) * 3) 이라고 할 수 있다. 즉 O(V) + O(V) * O(V)이고 시간복잡도 상으로는 O(V^2)가 된다.
최소힙 기반 우선순위 큐를 사용할 경우
위의 알고리즘에서 비효율적인 부분은 최소값을 찾는 부분일 것이다. 최소값을 찾는 가장 좋은 방법은 역시 최소힙을 사용하는 것이다. 최소힙을 사용하면 최소값을 찾는 연산이 O(V)에서 O(log V)로 줄어든다.
또 하나 중요한 포인트는, 각 노드를 방문해서 이웃 노드의 최소거리값이 업데이트될 때의 구현 방식이다. 아래 그림을 보자. queue 배열은 맨 처음에는 시작점인 1을 제외하고 나머지 노드들까지의 거리는 무한대로 초기화되어 있다. 여기서 1번 노드를 방문하면 1번 노드와 연결되어 있는 2번 노드까지의 최소거리값이 1임을 알 수 있게 된다.

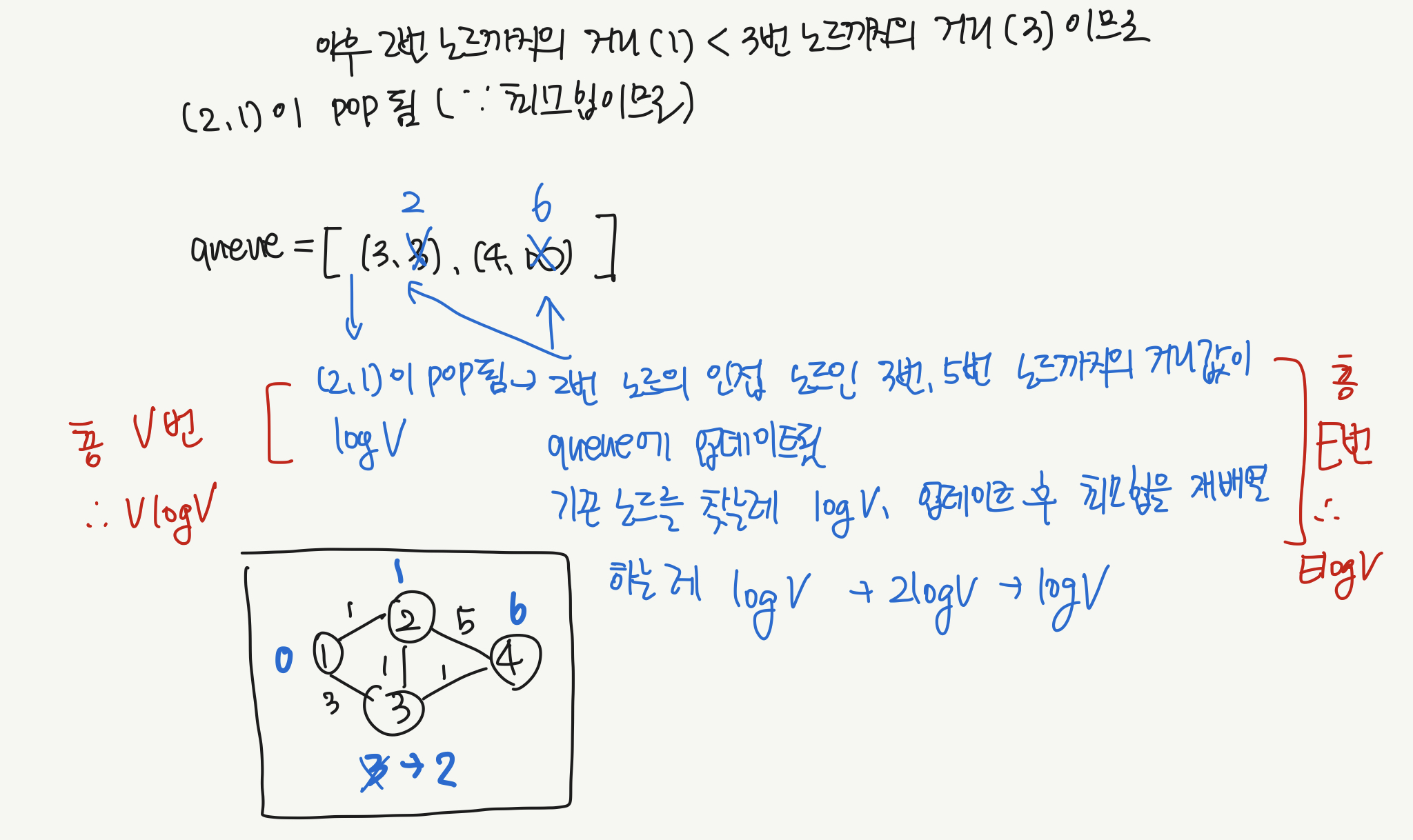
일반적으로 그냥 리트코드에서 다익스트라 문제 풀 때는 최소힙이라 어차피 최소값이 pop 되니까 새로운 거리값을 queue에다가 그냥 쭉쭉 넣었는데, Introduction To Algorithms 같은 책에서는 기존 데이터의 거리값을 업데이트하는 방식으로 설명하고 있다. 이 부분에 대한 설명이 여기저기 찾아봐도 조금 불명확한데, 우선 힙에서 특정 노드의 값을 찾는 연산 + 해당 값의 거리값을 업데이트하고 다시 최소힙을 규칙에 맞게 정렬하는 연산으로 나누어 생각해 보았다.
위 그림에서 2번 노드를 방문해 3, 4번 노드를 업데이트 하는 과정을 보자. 최소힙에서 특정 노드의 위치를 탐색하는 데에는 log V만큼의 시간이 걸린다. 그리고 거리값이 업데이트 되었으므로 최소힙의 순서를 재배치해야 할 수 있다. 이 경우에도 최대 log V가 걸린다. 2logV이므로 logV로 간략화할 수 있다. 이후에 queue를 한번 더 pop하면, 의 최소값인 (3, 2)가 pop되고, 거리 2를 기준으로 3번 노드의 인접 노드를 탐색하게 될 것이다. 2번은 이미 방문했기 때문에 넘어가고, 4번 노드까지의 거리가 3으로 업데이트될 것이다.
즉, 최소힙 기반 구현은 1) 현재 힙에서 거리가 가장 작은 정점의 값을 pop하고(log V) 2) BFS 형태로 인접 노드를 탐색해 방문하지 않은 노드를 찾은 후, queue에서 해당 노드를 검색해 그 거리값을 업데이트한다. (log V) 1)은 총 정점의 개수만큼 이뤄지고, 2)는 그래프 전체의 간선 개수만큼 이뤄진다. 정점의 개수를 V라 하고 그래프의 총 간선 개수를 E라고 하면 이 일련의 과정은 Vlog V + Elog V이고, 따라서 (V + E)log V이다. 그래프 전체의 간선 개수 E는, 중간에 끊기는 정점이 없다는 가정 하에 E >= V - 1이므로 O((V + E)log V)는 O(E log V)로 간략화할 수 있다. 어차피 E가 V보다 크거나, E가 아무리 작아봐야 (V - 1)과 같기 때문이다.
이와 과정을 거치면 위에서 <파이썬 알고리즘 인터뷰>를 인용한 내용과 같아진다. 이걸 이렇게 2줄로만 띡 써 놓으면 당연히 이해가 안 되지... 하고 생각하기로 했다!
참고 자료
- Understanding Time Complexity Calculation for Dijkstra Algorithm (Baeldung)
- Understanding Time complexity calculation for Dijkstra Algorithm (Stack Overflow)
- <Introduction to Algorithms>, Thomas H Cormen 외
'CS' 카테고리의 다른 글
| 백만 개 row를 수정하다가 트랜잭션을 롤백한다면? (2) | 2022.08.22 |
|---|---|
| 외계어 같은 git 메시지들을 이해해 보자 (3) | 2022.08.07 |
| 관계형 모델은 DB를 어떻게 바꾸었을까? (0) | 2022.05.09 |
| "컴파일은 됐는데 실행하다 뻑난다"의 의미 (0) | 2022.02.25 |
| 재귀함수는 스택 메모리에서 어떻게 동작할까? (0) | 2022.02.18 |



댓글